机器学习-理解ROC、AUC以及rank-loss

理解ROC、AUC以及rank-loss

ROC

理解：以ROC在医学检测中的应用举例，首先我们需要将混淆矩阵中的各个元素赋予对应的含义。

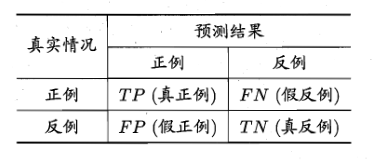
在医学检测中，我们可以按照下面的含义解释上述各元素（正例为阳性-得病，反例为阴性-健康）

• TP：预测结果是正例，真实情况是正例，可以看作是医生正确诊断出病例
• FN：预测结果是反例，真实情况是正例，可以看作是医生漏诊，将得病诊断为健康
• FP：预测结果是正例，真实情况是反例，可以看作是医生误诊，将健康诊断为得病
• TN：预测结果是反例，真实情况是反例，可以看作是医生检查出没有得病

我们再来看ROC中的TPR和FPR。 \[ TPR = {TP \over TP + FN} \]

\[ FPR = {FP \over TN + FP} \]

• TPR：\[真正例 \over 真实情况是正例\]即在所有实际为正例的样本中，被正确地判断为正例的比率，可以看作是在所有得病的人中，有多少人被医生正确地诊断出阳性。
• FPR：\[假正例 \over 真实情况是反例\]即在所有实际为反例的样本中，被错误地判断为正例的比率，可以看作是在所有健康的人当中，有多少人被医生误诊为得病。

那么对于一个机器学习的学习器而言，我们希望的是TPR越高越好，而FPR越低越好。然后实际情况是，当我们的阈值减小时，TPR和FPR会同时增大，当阈值为0的时候，即所有的实例都被预测为正例，此时的TPR为1，因为所有的阳性都被诊断出来了；此时的FPR为1，因为所有健康的人都被诊断为阳性。

ROC曲线就是以TPR为纵轴，以FPR为横轴，如图。

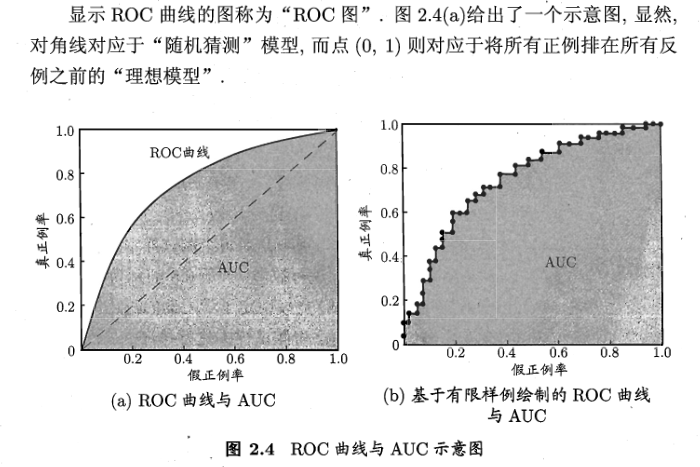
如图可见，如果想要TPR尽可能的高，那么相应的阴影部分的面积也会增大。我们进行学习器的比较时，与P-R图相似，若一个学习器的ROC曲线被另一个学习器的曲线完全”包住“，则可断言后者的性能优于前者；若两个学习器的ROC曲线发生交叉，则难以一般性地断言两者孰优孰劣。此时如果一定要进行比较，则较为合理的判据是比较ROC曲线下的面积，即AUC（Area Under ROC Curve）。

这里的AUC的公式比较好理解，就是通过坐标计算出一小块一小块的面积的和。

ROC曲线可能出现的3种情况

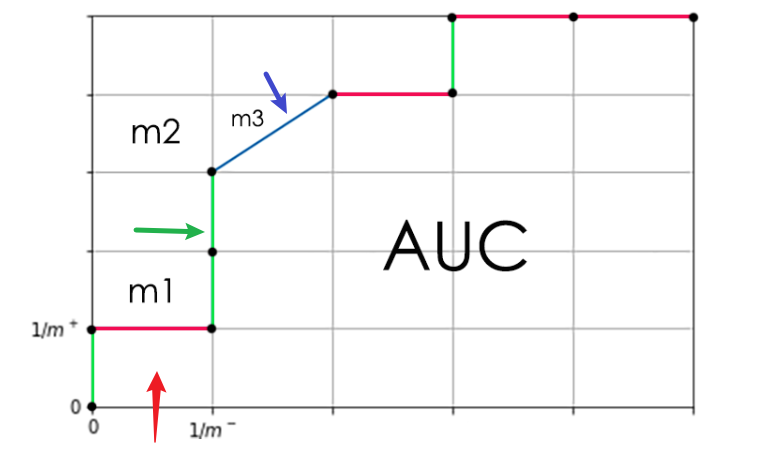
对应3种情况：

1. 如果\[y_i = y_{i+1}\]那么小块形状是矩形，真正例率不变，假正例率增加\(1 \over m-\)，水平向右移动，面积就是$(x_{i+1} - x_i) y_i $
2. 如果\(x_i = x_{i+1}\)那么小块形状是垂直的线段，真正例率增加\(1 \over m+\)，假正例率不变，垂直向上移动，面积就是0
3. 如果下一个点\((x_{i+1}, y_{i+1})\)\(在\)\((x_{i}, y_{i})\)\(的右上方，真正例率和假正例率同时增加，面积按照梯形面积公式计算，\)\({1\over2}\cdot(x_{i+1}-x_i)\cdot(y_{i+1}-y_i)\)

综上，总的AUC计算公式，如下。

这里引入了一个loss