3D gaussian splatting
3D gaussian splatting
前置知识
球谐函数
我们在学习高等数学的时候都学习过傅里叶，任何一个二维函数都可以分解成为不同的正弦与余弦之和：
\(f(x)=a_0+\sum_{n=1}^{+\infty}a_ncos\frac{n\pi}{l}x+b_nsin\frac{n\pi}{l}x\)
这里\(cos\frac{n\pi}{l}x\)和\(sin\frac{n\pi}{l}x\)就叫作基函数，原则上来讲当\(n->+\infty\)时，我们就可以完美拟合这个函数，即使只有有限个\(n\)，我们也可以对这个函数进行近似。 \(f(x) \approx
a_0+\sum_{n=1}^{i}a_ncos\frac{n\pi}{l}x+b_nsin\frac{n\pi}{l}x\)
这种基函数的思想其实在数学中很常见。
我们考虑一个有界，闭合的，平滑的曲面。 
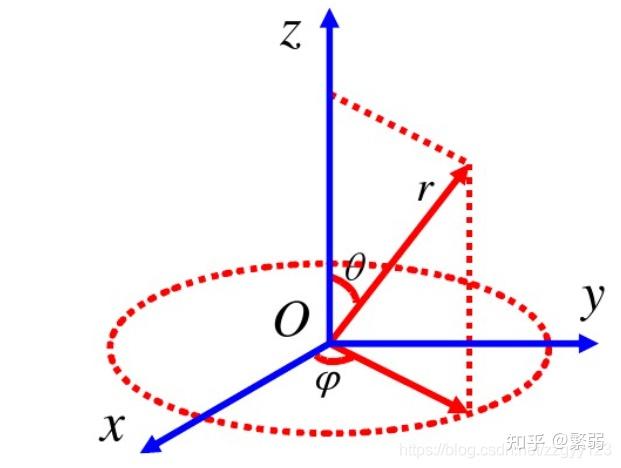它可以用球面函数表示方法来表示\(f(\theta,\phi)\)，这样一个函数同样可以有自己的基函数来组成。
它的基函数长这样： 
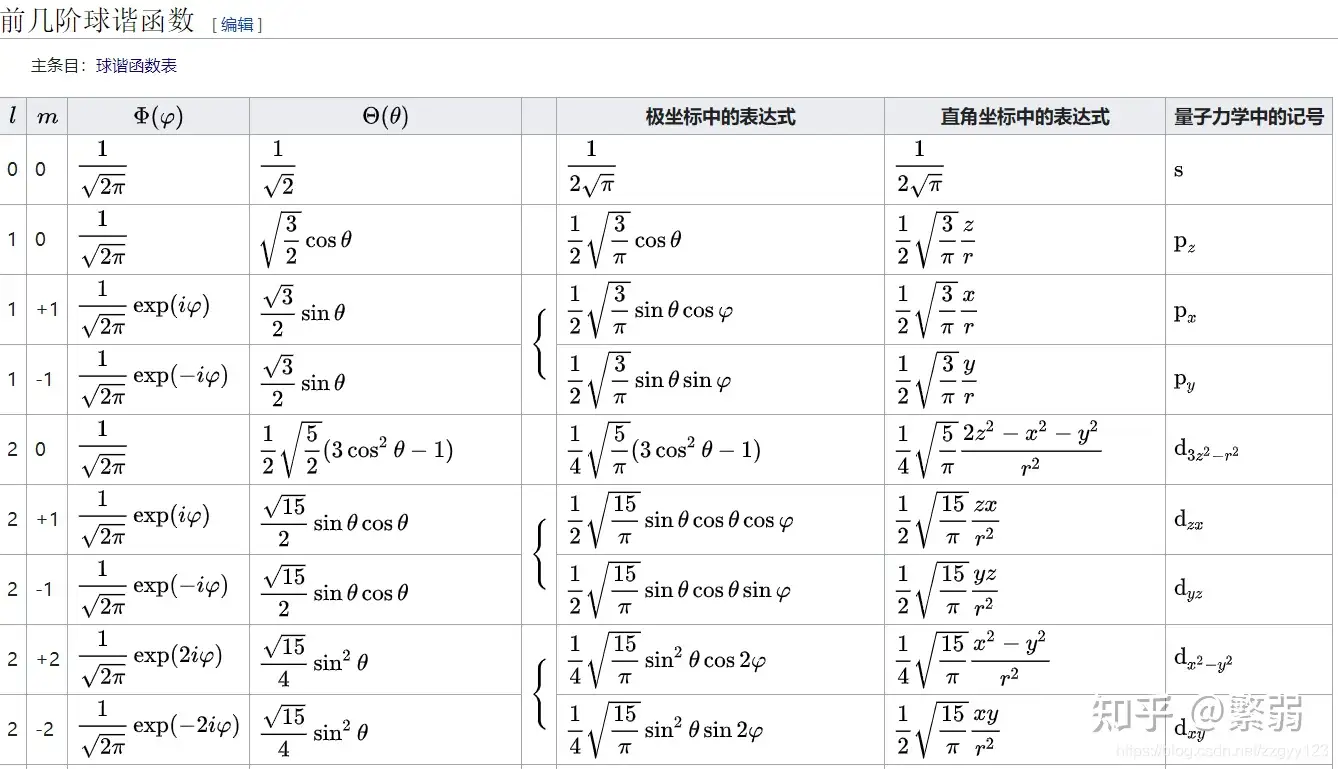因此，我任意一个球面坐标的函数，就可以用多个球谐函数来近似。 \(f(\theta,\phi) \approx
a_0f_{l=0,m=0}f(\theta,\phi)+a_1f_{l=1,m=-1}f(\theta,\phi)+a_2f_{l=1,m=0}f(\theta,\phi)+a_3f_{l=1,m=1}f(\theta,\phi)+a_4f_{l=2,m=-2}f(\theta,\phi)+a_5f_{l=2,m=-1}f(\theta,\phi)+...\)
如果想要近似准确点，就多用一些level的球谐函数，如果不需要太准确，用较少的球谐函数就可以。
### 3D Gaussian #### 一维高斯分布 一维高斯的概念我们都很熟悉，公式为：
\(p(x)=\frac{1}{\sqrt {2
\pi}\sigma}e^{-\frac{(x-u)^2}{2 \sigma^2}}\) 其图像如下：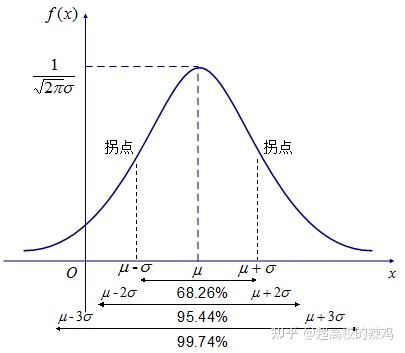 
其均值为\(u\)，方差为\(\sigma\)，数据会以99%的概率落在\(u-3\sigma\)到\(u+3\sigma\)之中。 #### 三维高斯分布
多维高斯的公式如下： \(\frac{1}{(2
\pi)^{\frac{N}{2}}|\Sigma|}e^{-\frac{1}{2}(x-u)^T\Sigma^{-1}
(x-u)}\) 这个三维高斯画出来的图是什么样的呢？
我们想像一下固定概率为\(p\)的三维高斯分布长什么样。 \(\frac{1}{(2
\pi)^{\frac{N}{2}}|\Sigma|}e^{-\frac{1}{2}(x-u)^T\Sigma^{-1}
(x-u)}=p\) \(-ln(2
\pi)^{\frac{N}{2}}|\Sigma|-\frac{1}{2}(x-u)^T\Sigma (x-u)=lnp\)
\((x-u)^T\Sigma (x-u)=-2lnp-2ln(2
\pi)^{\frac{N}{2}}|\Sigma=C\) 这里，\(\Sigma\)是一个实对称矩阵，令： \(\Sigma=P^T\wedge P\) \((x-u)^TP^T\wedge P(x-u)=(P(x-u))^T \wedge
P(x-u)=C\) 令: \(y=P(x-u)\), 令
\[
\wedge=
\begin{bmatrix}
\sigma_1^2 & 0 & 0\\
0 & \sigma_2^2 & 0 \\
0 & 0 & \sigma_3^2
\end{bmatrix}
\] 原式子变为 \[
y^T \wedge y=\sigma_1^2y_1^2+\sigma_2^2y_2^2+\sigma_3^2y_3^2
\]
这是一个标准的椭球的方程，所以原式子就是把标准椭球先经过经过一个旋转变换\(P^{-1}\)，再挪到\(u\)点得到。所以对于一个三维高斯而言，同一个椭球表面其概率密度相同，离\(u\)越远，其概率越小。 
所以一个多元高斯轴的长度为\(\Sigma\)的特征值。
跟一维一样，有99%的概率落在3倍方差之内，也就是有99%的概率落在\(3\sigma_1,3\sigma_2,3\sigma_3\)所在的椭球内，另外\(\sigma_1,\sigma_2,\sigma_3\)为\(\Sigma\)的特征值。 ### 图形学渲染-坐标变换
在传统图形学的渲染pipeline里面，需要把空间里面的物体投影到相机的平面，也就是需要知道空间中每个点投影到特定相机平面上的位置是多少，在传统图形学里面的流程通常是这样的：
先把视椎内物体进行一个透视投影，压缩到一个非透视的空间内，然后使用正交投影，将视椎内物体压缩到各维度为[-1,1]的空间内。
#### 透视投影 
设近平面为\(n\)，远平面为\(f\)，这里假设我们相机坐标的位置如下（采用右手坐标系）：
空间内任一点\((x,y,z)\)投影到相机平面的位置为\((x',y',z')\)，投影矩阵为\(P\), 则有： \(x'=\frac{n}{z}x,y'=\frac{n}{z}y\)
换成齐次坐标表示，也就是经过。 \([x,y,z,1]^T->[nx,ny,?,z]\) \[
P=
\begin{bmatrix}
n && 0 && 0 && 0\\
0 && n && 0 && 0\\
? && ? && ? && ?\\
0 && 0 && 1 && 0
\end{bmatrix}
\] 我们还有两个约束条件，在近平面上，所有点的\(z\)坐标不会变，都为\(n\)，在远平面上，所有点的\(z\)坐也不会变： \([x,y,n,1]->[nx,ny,n^2,n]\) \([x,y,f,1]->[x',y',f,1]=[\frac{nx}{f},\frac{ny}{f},f,1]=[nx,ny,f^2,f]\)
所以\(P\)一定满足如下的形式： \[
P=
\begin{bmatrix}
n && 0 && 0 && 0\\
0 && n && 0 && 0\\
0 && 0 && A && B\\
0 && 0 && 1 && 0
\end{bmatrix}
\] 其中\(An+B=n^2\),\(Af+B=f^2\) 解出来为： \(A=n+f, B=-nf\) 因此，投影距离为： \[
P=
\begin{bmatrix}
n && 0 && 0 && 0\\
0 && n && 0 && 0\\
0 && 0 && n+f && -nf\\
0 && 0 && 1 && 0
\end{bmatrix}
\] #### 正交投影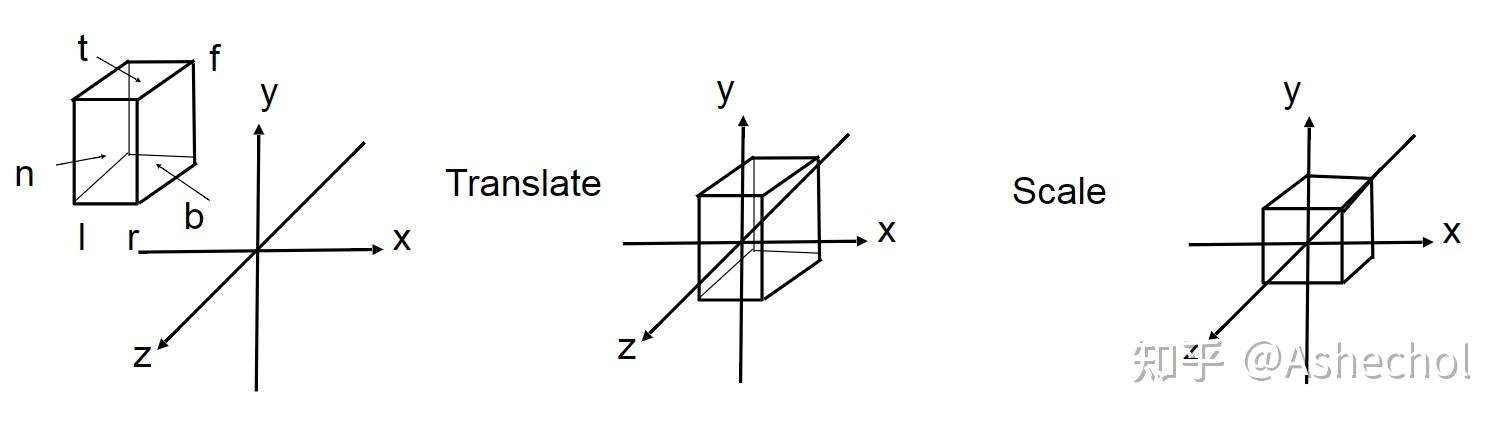 
下交投影相对较简单，只需要将非透视空间内的内容挪到坐标原点，并规范化到[-1,1]的空间内，设x坐标的范围为[l,r]，y坐标为[b,t]，z坐标为[n,f],
我们可以先把坐标得到了零点，再做各个维度的压缩，从坐标到零点的变换矩阵为：
\[
T_1=
\begin{bmatrix}
1 & 0 & 0 & -\frac{l+r}{2}\\
0 & 1 & 0 & -\frac{t+b}{2}\\
0 & 0 & 1 & -\frac{n+f}{2}\\
0 & 0 & 0 & 1\\
\end{bmatrix}
\] 缩放矩阵如下： \[
T_2=
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & 0\\
0 & \frac{2}{t-b} & 0 & 0\\
0 & 0 & \frac{2}{n-f} & 0\\
0 & 0 & 0 & 1\\
\end{bmatrix}
\] 最后的矩阵就是两个矩阵乘起来： \[
T=T_2T_1=
\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\
0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f}\\
0 & 0 & 0 & 1\\
\end{bmatrix}
\] 综合一下，将一个坐标先经过矩阵\(P\), 再过\(T\)的变换就可以变到NDC坐标系。 ###
基于点的渲染
这块不大熟，根据论文做个粗浅的理解，图形学里面有时候会对一些离散的点数据进行渲染（点云），因为点是没有体积的，所以我们可以有一个固定的几何表示（球，立方体）来对这个点进行表示，以球为例，投影到相机面上变会成一个圆，然后着色时，如果一个像素点上，有几个点都投影过来了，这时候使用\(\alpha\) blending. \(C=\sum_{i=N}c_i \alpha_i
\prod_{j=1}^{i-1}(1-\alpha_j)\)
这个公式其实跟神经辐射场推出来的离散公式也非常的像。 ## Gaussian
Splatting
回想一下传统神经辐射场，我们将三维空间里连续数据存下来，然后使用体渲染公式，得到某一个像素点的颜色，由于空间中物体的通常是稀疏的，MLP里存放的三维体数据很多其实都存在浪费，另外ray
matching的方法使得渲染速度变得相当地慢。像Instant
NGP采用了hash表的方式，来减少无效数据的存放，Plenoctrees采用了八叉树来减少数据存放，但这些方法并没有改进ray
marching。而且像Instant
NGP因为人为缩小了存放的空间，所以实际是一种渲染质量对时间的妥协。
所以，如果我们能够设计一种算法，能够自适应的学习三维空间里面物体的分布，同时可以减去ray
marching这一繁琐的采样步骤，那理论上来说，就可以一定程度上解决现在nerf的问题。
我们把Nerf的场景想像成一个非常非常密集的点，我们需要存储的点的信息，其实只会是那些在物体表面上的，因此我们能不能只存那些有物体地方的点呢，让神经网络去学习这些点的坐标与颜色，透明度等等，然后用基于点的渲染方式进行渲染，将渲染后的图片与图片计算损失函数，最后得到这些点的坐标，颜色与透明度。
### 如何对点进行初始化 #### 随机初始化 #### sfm 
### 点体积的扩展 跟particle-based
rendering一样，因为点没有体积，所以需要对它进行一个扩展，扩展方式这篇论文与传统的particle-based
rendering不一样，它用的3D Gaussian表示。 \(G(x)=e^{-\frac{1}{2}x^T\Sigma^{-1}x}\) 
这跟前面3D
Gaussian里的表示是一样的，只是省去了前面的常数项。跟前面那这球或者方形的表示不同，3D
Gaussian这种表示具有更强的灵活性，它可以用较少的点表示更复杂的形状。
在这种表示下面，我们希望存储的信息就变成了： 1. 每个点的坐标； 2.
每个点的高斯表示中的\(\Sigma\); 3.
每个点的颜色； 4. 每个点的不透明度\(\alpha\)； 这里的\(\Sigma\)（协方差矩阵）是一个半正定矩阵，所以你当然不能对这个随机对这个距离进行初始化，然后随机迭代，因为要保证半正定这个条件，我们假定：
\(\Sigma=P \wedge P^T=P
\wedge^{\frac{1}{2}}\wedge^{\frac{1}{2}}P^T=(P \wedge^{\frac{1}{2}})(P
\wedge^{\frac{1}{2}})^T\). 其中，\(P\)是一个正交阵，可以理解为是一个旋转矩阵，\(\wedge^{\frac{1}{2}}\)为一个全为正数的对角阵，可以理解为是一个scale矩阵，论文里的表示为：
\(\Sigma=RSS^TR^T\) ### 点的颜色的表示
我们在Nerf里面为了去模拟一些高光的点，会入view dir，也不是不同view dir,
其看过来颜色是不一样的，之前都用神经网络来存这一信息.
那我们现在存的话怎么存，使用球谐函数，这其实是很多nerf都采用的存储方式。
### 如何投影
那怎么知道空间里面一个高斯投影到某个相机平面上，在相机平面上的什么位置呢？这里采用了跟之前NDC坐标有点类似的方法，使用“挤压”的方式，相机坐标\((t_1,t_2,t_3)\)压缩到\((x_1,x_2,x_3)\)上。 \[
x_1=\frac{t_1}{t_3}\\
x_2=\frac{t_2}{t_3}\\
x_3=\sqrt{t_1^2+t_2^2+t_3^2}
\] 这里\(x_3\)设计成是因为在基于点的着色时，需要考虑一个射线出去的点的前后顺序，所以需要对相应位置进行保留。但是比较遗憾的是，这并不是一个线性变换，也就是无法通过求解一个变换矩阵把这个变换求解出来。但是我们可以使用一个线性变换对这个非线性变换进行近似。我们已经在高数中学过泰勒展开式：
\(f(x) \approx
f(x_0)+f'(x_0)(x-x_0)\) 这里的情况其实当函数为\(R->R\)的情况，如果把这个扩展到高维呢\(R^m->R^n\)。 \(f(\bold x)=f(\bold x_0)+\bold J (\bold x-\bold
x_0)\) 这里\(J\)雅可比矩阵，可以看来一阶导的多维形式，假设我们输入为:\(x_1,x_2,...x_m\),输出为\(y_1,y_2,...,y_n\) \[
J=
\begin{bmatrix}
\frac{\partial y_1}{x_1}&&\frac{\partial
y_1}{x_2}&&...&&\frac{\partial y_1}{x_m}\\
\frac{\partial y_2}{x_1}&&\frac{\partial
y_2}{x_2}&&...&&\frac{\partial y_2}{x_m}\\
...\\
\frac{\partial y_n}{x_1}&&\frac{\partial
y_n}{x_2}&&...&&\frac{\partial y_n}{x_m}
\end{bmatrix}
\] 前面的非线性变换，使用这种方式进行近似的话，其雅可比矩阵为：
\[
\begin{bmatrix}
\frac{1}{t_3} && 0 && -\frac{t_1}{t_3^2}\\
0 && \frac{1}{t_3} && -\frac{t_2}{t_3^2}\\
\frac{t_1}{\sqrt{t_1^2+t_2^2+t_3^2}} &&
\frac{t_2}{\sqrt{t_1^2+t_2^2+t_3^2}} &&
\frac{t_3}{\sqrt{t_1^2+t_2^2+t_3^2}}
\end{bmatrix}
\]
我们可以对每个高斯在其中心点展开，得到其雅可比矩阵，就可以得到这个高斯的线性变换矩阵。因为高斯分布的性质，如果一个线性变换\(Ax+b\)，高斯分布经过这个变换之后： \[
u'=Au+b
\] \[
\Sigma'=A \Sigma A^T
\] 所以一个世界坐标系下均值点为\([t_1,t_2,t_3]\)，方差为\(\Sigma\)的高斯经过这个变换后，会变为均值为\([x_1,x_2,x_3]\)，方差为\(\Sigma'=JW \Sigma
W^TJ^T\)，其中这里\(W\)为世界坐标到相机坐标的转换。
经过这个变换之后，我们只要丢掉\(\Sigma'\)的第三行的第三列就是投影到相机平面的协方差矩阵。
### 像素点着色
要计算像素点的着色，首先需要知道哪些高斯投影到这个像素点上，我们通过之前的计算已经知道空间里的一个高斯投影到相机平面上是一个什么新的高斯，通过前面对高斯的计算，我们也知道有99%的概率会落在\(3\sigma_1,3\sigma_2\)之内，所以如果一个像素落在高斯的区间内，那我们认为这个像素被高斯所覆盖，为了简化计算，我们将范围扩大为\((max(3\sigma_1,3\sigma_2),max(3\sigma_1,3\sigma_2))\)
。到这里其实我们已经知道一个像素被哪些高斯覆盖了，论文里在这一步使用了一些加速的技巧。
首先可以通过之前的计算，得到每个高斯覆盖的范围，对整个空间内的高斯进行排序。将空间分为一个一个tile，可以得到覆盖这个tile的高斯。对一个tile里的每个像素，计算tile中每个高斯对它的贡献度以及其透明度：
\[
p_i\alpha_i \prod_{j=1}^{i-1}(1-p_i\alpha_j)
\] 这里: \[
p_i=e^{-\frac{1}{2}x^T\Sigma'^{-1}x}
\]
这里tile和像素点颜色的计算使用了cuda进行编写，使用了并行计算，这是Gaussian
得以提高的原因。 ### Adaptive Control 
因为3D
Gaussian的方法是对多个高斯进行优化，高斯的数量的设定当然很重要，如果是一个很简单的场景，少量高斯的数量应该就可以，但是如果是一个很复杂的场景，高斯的数量就需要增加，一个比较好的方法就是我们可以自适应来生成高斯的数量，因此，论文里有提到一个adaptive
control的方法。 每隔一定的训练时间(100 iter or 100
iter)。会根据目前的情况决定哪些高斯应该被去除，哪些部分应该增加高斯表示。
1. 哪些需要去掉？ 透明度非常低的（\(\alpha\)低于某个阈值的），离相机距离非常近的（很可能是floater）。
2. 其它
另外对于一些表示过多或者不够的地方，也需要进行自适应调整，怎么算表示过多或者不够呢？这些地方通常是坐标梯度较大的地方，梯度较大，表示这里高斯表示其实不太合适，模型试图移动这些点，改善模型的表示，所以可以设置一个梯度的阈值，找到这些表示不好的地方。
### 训练&损失函数 
\(L=(1-\lambda)L_1+\lambda
L_{D-SSIM}\)