F1度量为何用调和平均而不用算术平均

P-R图

查准率P（Precision）和查全率R（Recall）是一对矛盾的度量，一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

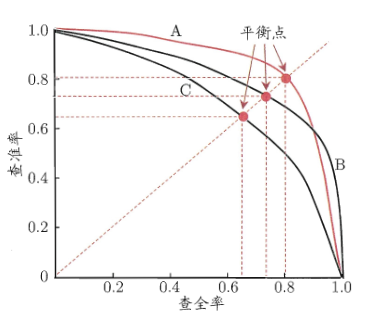
\(F_1值\)

当我看到西瓜书这个地方的时候，觉得一切都很有道理，但是突然又觉得不讲道理。虽然我知道F1度量肯定是人为规定的一个式子，但是为什么F1度量用的是调和平均，为什么不简单的使用算术平均或者其他的平均式综合考虑查准率和查全率。

书上的解释是与算术平均（\(P + R \over 2\)）和几何平均（\(\sqrt{(P \times R)}\)）相比，调和平均更重视较小值。

于是我又去看了吴恩达的机器学习课程的相关内容，才算是搞懂了。

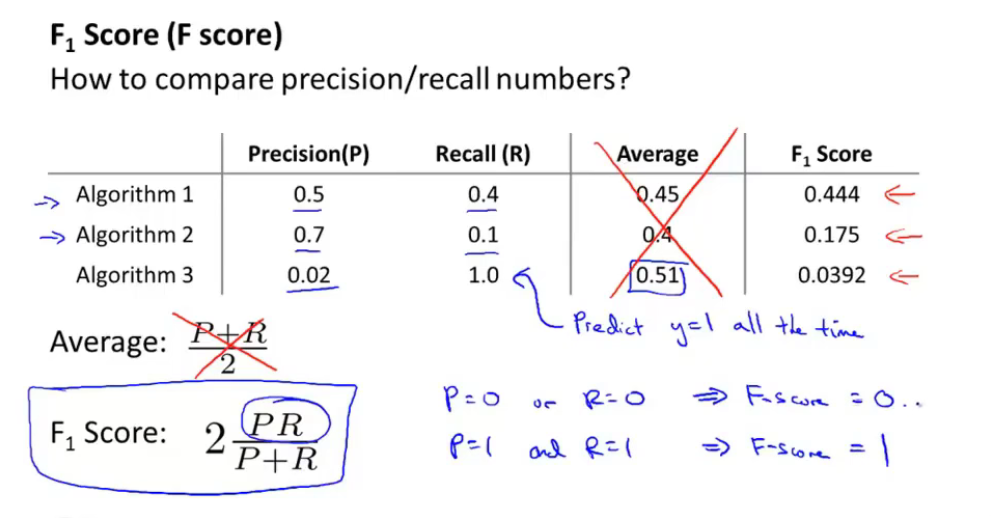
如果我们有不同的算法，我们如何比较不同的查准率和召回率。具体一点，假设我们有三个不同的学习算法，或者这三个不同的学习曲线是同样的算法但是临界值（Threshold）不同，我们怎样决定哪一个算法是最好的？

我们可以用一个评估度量来决定算法的优劣。那么我们怎么得到一个评估度量值呢？

你可能会去尝试的一件事情是计算一下查准率和召回率的平均值（算术平均） \[ Average = { P + R \over 2} \] 但是这可能并不是一个很好的解决办法。因为，如果我们的回归模型总是预测y = 1（阈值很低），那么你可能得到非常高的召回率，得到非常低的查准率。相反地，如果你的模型总是预测y = 0，就是说，如果很少预测y = 1，对应的，设置了一个高临界值，最后你会得到非常高的查准率和非常低的召回率。这两个极端情况，一个有非常高的临界值，一个有非常低的临界值，它们中的任何一个都不是一个好的模型。我们可以通过非常低的查准率或者非常低的召回率，判断这不是一个好模型。如果你只是使用\(P + R \over 2\)，算法3的这个值是最高的。即使你可以通过使用总是预测y = 1这样的方法来得到这样的值，但是这并不是一个好的模型。算法1和算法2比算法3更好，但是在这个例子中，查准率和召回率的平均值，算法3是最高的。

因此我们通常认为查准率和召回率的平均值（算术平均）不是评估算法的好方法。相反地，有一种结合查准率和召回率的不同方式，叫做F值，公式是 \[ F_1Score = 2{ PR \over P + R} \] 我们可以通过\(F_1Score\)来判断算法1有最高的F值，算法2第二，算法3是最低的。因此，通过F值我们会在这几个算法中选择算法1。F值也叫做\(F_1\)值。它的定义会考虑一部分查准率和召回率的平均值，但是它会给查准率和召回率中较低的值更高的权重。因此，你可以看到F值的分子是查准率和召回率的乘积，因此如果查准率等于0，或者召回率等于0，F值也会等于0。因此它结合了查准率和召回率，对于一个较大的F值，查准率和召回率都必须较大。

有较多的公式，可以结合查准率和召回率，F值公式只是其中一个，但是处于历史原因和习惯问题，人们在机器学习中使用F值。这个术语F值，没有什么特别的意义。

总结

后续我又上网搜索了下别人对算术平均和调和平均的理解

算术平均值是一个良好的集中量数，具有反应灵敏、确定严密、简明易解、计算简单、适合进一步演算和较小抽样变化的影响等特点。但是极易受极端数据的影响，每个数据的或大或小的变化都会影响最终结果。

调和平均数具有以下几个主要特点：

1、调和平均数易受极端值的影响，且受极小值的影响比受极大值的影响更大。

2、只要有一个标志值为0，就不能计算调和平均数。

3、当组距数列有开口组时，其组中值即使按照相邻组距计算，假定性也很大。

4、调和平均数应用的范围较小。